The Perihelion Advance Formula from Lorentzian Principles

There are three well-known tests of general relativity (GR) proposed by Einstein: the extra bending of light rays passing near the Sun, the slowing of clocks immersed in a gravitational potential, and the advance of the perihelion of planet Mercury. In the 1960s, Irwin Shapiro added a fourth test, the slowing of radar signals through the Sun's field. [See Shapiro et al., 1971.] It was well known even to Sir Arthur Eddington (1920) that some of these results were also predicted by aether theories. However, that was not known to be true of the advance of the perihelion of Mercury, which seemed by far the most impressive prediction of the theory.

Imagine a tangible but presently undetectable light-carrying-medium (LCM) surrounding the Sun, whose density varies with the Sun's gravitational potential. As a light wave passes through such a medium, it will be bent by refraction away from a radial vector outward from the Sun. This is because the wave's propagation speed is slower where the medium is denser. In standard GR, the Einstein curvature tensor is interpreted to indicate the curvature of space-time. If it is instead interpreted as the density of a medium varying with the Sun's gravitational potential, then the mathematical formalism is identical, and the correct light bending amount by refraction is predicted. (See Eddington, 1920.)

In a similar way, all electromagnetic phenomena must propagate through the LCM with speeds that slow where the medium is denser. Hence, the slowing of radar signals and of atomic clocks in a gravitational potential are predicted with equal ease. (See Hatch, 1999.) Our task here will be to determine if the same principles apply to predicting perihelion advance, or if that phenomenon is unique to GR.

"Perihelion", of course, refers to the point in an elliptical orbit that is closest to the Sun. Our developments here will apply more generally than just the solar system, so, strictly speaking, we should use the generic expression "pericenter". However, since we intend to focus on applications to the planet Mercury, we will continue to speak of the "perihelion" advance formula.

For Mercury, and in general for all orbits that are nearly ellipses, the basic form of a formula for perihelion motion is always the same, being governed by the properties of orbital motion on an ellipse. Perturbations that are themselves modulated by the size and shape of the elliptical orbit and by the speed of a body traveling along that ellipse generally change perihelion motion by simple integer multiples of the basic form. This basic form (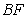) is:

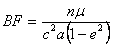
where 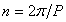is the orbital mean motion of the planet, 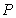is its orbital period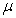, is the product of the gravitational constant and the mass of the Sun, 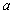is the semi-major axis (mean distance) of the orbit, 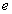is orbital eccentricity, and 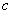= speed of light. We will show the derivation of this basic form below.

The nature of this basic form is such that parameter-free perturbations are nearly all constrained to produce perihelion motions that are integer (or at worst, half-integer) multiples of it. (This is to be contrasted with parameterized perturbations, for example those resulting from some undiscovered mass or force, that are proportional to some free parameter.) The observed perihelion advance for Mercury is three multiples of the basic form,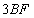 , to within the error of observations.

In GR, the correct multiplier of 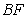is arrived at by combining three contributions. The first is the effect of "time dilation", which contributes 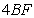. The second is the effect of "space contraction", which contributes 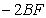. The third is the effect of mass or momentum increase with speed, which contributes 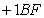. The sum of these three contributions gives the observed amount, 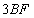. Einstein, of course, knew the observed amount in advance, and had the opportunity to combine various effects in various ways until the correct answer was obtained. It is curious that Einstein required a combination of three effects, with one of them canceling 40% of the contribution of the other two. Clearly, there was ample room to argue for a different combination if Mercury's actual perihelion motion had been different.

By contrast, aether theories have no such freedom. There is no "time dilation", only clock slowing; and that has no direct effect on the perihelion motion. There is no "space contraction", only meter stick shrinkage; and that has no effect on the perihelion motion. Likewise, just as Mercury's own mass makes no significant contribution to its own perihelion motion, any mass or momentum change for Mercury should have no effect on its perihelion motion. Indeed, if matter could always be treated as an ensemble of particles with purely ballistic motion, aether theories would not contribute anything to perihelion advance.

However, electrons are not particles with purely ballistic motion. Electrons have primarily wave-like properties, and are the main reason that light is considered an "electromagnetic" phenomenon. Indeed, one of Louis de Broglie's chief contributions to physics was demonstrating that ordinary matter has wave properties too. We are therefore obliged to consider that orbiting bodies will be influenced by the density of the LCM that they travel through because of the influence of the LCM on their electrons.

Understanding the effect of the LCM on perihelion motion geometrically is simple. The elliptical motion of orbiting bodies is slowed most by the LCM near perihelion, where that medium is densest; and is slowed least near aphelion, where the LCM is sparsest. This velocity imbalance (slower at perihelion, faster at aphelion) rotates the ellipse forward, which is what an advance of perihelion means. See Figure 1.

For a more detailed understanding, we begin by noting that the velocity of anything propagating through a medium is inversely proportional to the square root of medium density -- a general wave property derived in many elementary physics texts. When comparing observable phenomena for a stationary body at different gravitational potentials, the relativistic clock-slowing, meter-stick-contraction factor is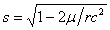 , where 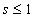and the gravitational potential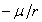, (where 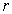is distance from the Sun), is proportional to changes in medium density.

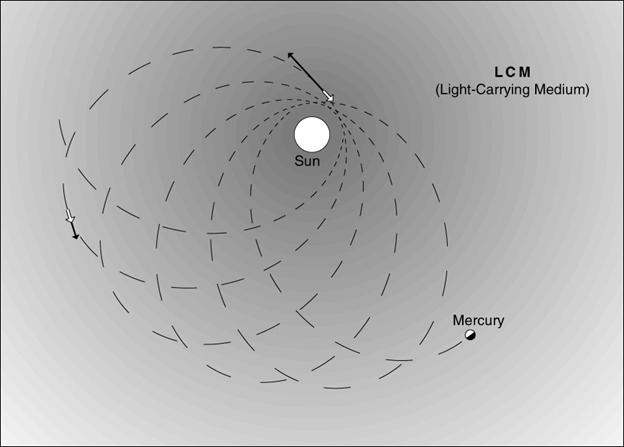
Figure 1. The weaker-than-average light-carrying medium (gray) near aphelion adds a small velocity (white arrow) to the orbital velocity vector (black arrow). The denser medium near perihelion creates a net loss of orbital velocity. The combination rotates the ellipse (advances the perihelion). Copyright ©1999 by Boris Starosta, This email address is being protected from spambots. You need JavaScript enabled to view it.

Quoting the principles outlined by Eddington (1920): "Light moves more slowly in the material medium then in a vacuum, the velocity being inversely proportional to the refractive index of the medium. The phenomenon of refraction is in fact caused by a slowing of the wave-front in passing into a region of smaller velocity. We can thus imitate the gravitational effect on light precisely, if we imagine the space around the Sun filled with a refracting medium which gives the appropriate velocity of light. To give the velocity , the refractive index must be 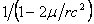, or, very approximately, 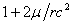." Note that Eddington's factor 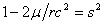in our notation.

These principles work well for purely wave phenomena. But for predominately ballistic motion, the effect of the LCM is to slightly slow the velocity that the orbiting body would otherwise have. The relativistic clock-slowing, meter-stick-contraction factor is 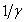, where 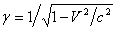, , and 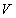is velocity. Analogous to wave velocities being slowed by the factor 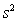, ballistic velocities are slowed by the factor 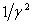. These two velocity-slowing effects are sufficient to explain all relativistic phenomena. 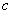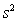To the accuracy we care about here, we can neglect the dependence of on , and 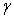assume that is independent of the density of the LCM.

A quantitative derivation of perihelion motion using celestial mechanics follows. Let 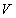be the orbital velocity of a massless body. Hence, if 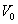is the orbital velocity the body would have in a Newtonian force field, the actual velocity of the massless body will be 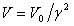. This slower-than-Newtonian velocity will give the false impression that the value of 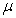for the Sun is smaller than it really is. That by itself does not disturb the elliptical orbit of the massless body. But because an orbiting body moves faster at perihelion than at aphelion, the factor by which it is slowed, 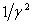, is smaller at perihelion than at aphelion. And this imbalance is solely responsible for the perihelion advance.

The extra slowing and speed-up of an orbiting body due to 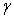varying as the body itself slows down and speeds up simulates an extra force acting on the body along the velocity vector. The formula for the change in Newtonian velocity is: 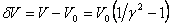. The derivative of this with respect to time is the extra acceleration directed tangent to the orbital velocity vector, , needed to produce the given change in velocity. We will compute , treat it as a perturbation, and plug it into standard celestial mechanics formulas to learn the effect it generates on the motion of the perihelion of the orbiting body.

Differentiating 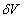with respect to time to get an expression for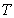, and expanding 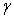into a series and retaining only the first term, we get

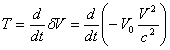
In this first-order approximation, it is safe to make no distinction between 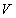and 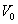because that would only lead to higher-order terms. This leads to:

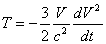
To make the derivative easier, we can substitute from the energy equation for orbits,

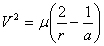
The needed derivative is

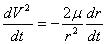
The new derivative for 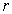can be found, for example, in equation (6.3.21) of Danby (1988), with the aid of the definition in equation (6.2.10):

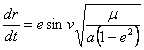
where 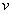is orbital true anomaly (the angle at the Sun between the perihelion and the orbiting body) . Making all these substitutions, we get our new expression for :

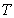Danby's equation (1.7.3) shows how to compute perihelion motion (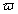 = longitude of perihelion) from a perturbation along the velocity component:

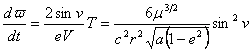
This has a secular and a periodic part. The periodic part gives rise only to small periodic variations. The secular part, of interest here because it builds progressively with time, comes from the time average value of 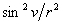, which is 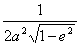by using Danby's equation (6.3.3). We will also need Kepler's law, . This gives the final form of the expression:

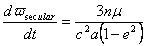
which is the same as Danby's equation (4.5.7).

We can apply this formula to Mercury by substituting the values from Table I, obtaining the result shown in the same table. This agrees with the observed rate of advance of Mercury's perihelion to within the ~ 1% errors of observation.

Because this formula for the perihelion advance of a massless orbiting body is the same as Einstein's formula, the most significant point of this derivation is that we have arrived at it from a single principle. We needed only ballistic velocity slowing by the factor 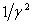, which immediately gave the correct multiple 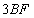; whereas Einstein needed to combine three components to get the correct formula. Moreover, our method invokes a tangential pseudo-force directed along the velocity vector; whereas two of Einstein's three components corresponded to radial pseudo-forces.

If the orbiting body had appreciable mass (as for binary pulsars), repeating the above derivation for each mass and combining the results yields an additional factor in the tangential force and in the final pericenter motion formula of

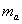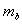where and are the separate masses. 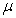is then the product of the gravitational constant times the sum of the masses.[1]

This factor reaches its minimum value of 0.5 when the two masses are equal. So the pericenter motion of equal-mass binary pulsars, for example, will be half what it would be if the same total mass were in a single body orbited at the same distance by a massless body. This is easy to understand using our single principle that masses propagate more slowly in a denser gravitational medium. If the two masses are equal, each moves with half the total relative velocity. So the velocity-slowing factor 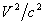will have one-fourth the size it would have for a massless body orbiting a single star. Because there are two masses each contributing one-fourth as much to the total perihelion advance, the net advance is raised back to one-half what it would be for the massless orbiter.

Although GR also predicts approximately one-half the pericenter advance for equal-mass stars, we might well raise an eyebrow at the unrelativistic nature of this mass factor. In effect, the velocity of each star with respect to the combined local gravity field affects the overall motion. The relativity principle would lead us to expect that only the relative velocity between the two stars would matter; but that is clearly not the case.

Indeed, the predicted pericenter motion is not identical for our velocity-slowing principle and for GR. For the Hulse-Taylor binary pulsar PSR 1913+16, the most extensively studied, general relativity predicts a pericenter advance rate of 4.23°/year. Our formula predicts 3.55°/year for the same orbital parameters.[2] This is a 16% difference. Such a large difference would certainly be observable. However, the matter is not so simple. We do not know the orbital parameters of the system, such as the star masses, the semi-major axis, or the orbit plane inclination. These must be solved for along with many other parameters, using the observations. Although the observations constrain certain parameter combinations very well, the individual parameters are often not so well constrained.

In the case in point, Damour & Taylor (1992) have remarked that the gravitational constant could be changed by 35% and still lead to solutions that satisfy all constraints. Using dots to denote time derivatives and 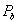for orbital period, their exact words are: "However, the 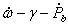test is a mixed test which combines strong-field and radiative effects in an indistinct way, so that one cannot logically conclude, when the test is satisfied, that both the specific strong-field and radiative predictions of general relativity have been independently confirmed. In fact, examples of theoretically well-motivated theories have recently been constructed … which have the same post-Newtonian limit as general relativity, and can pass the 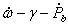test without fine-tuning, while still differing markedly from Einstein's theory because of the strong self-gravity effects in the pulsar and its companion. In extreme cases the three curves defined by 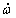, , and 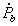can still meet within the observational precision, while the effective gravitational constant between the pulsar and its companion differs by as much as 35% from the usual Newtonian value."

This is equivalent to allowing the total system mass to change by 35%. A change of that size would change the pericenter rate by a comparable percentage. In short, if the system mass or other correlated parameters were changed within allowable limits set by the observations, the predicted pericenter motion using our velocity-slowing principle would rise to a value also consistent with observations. However, this indistinguishability of predictions will not last indefinitely. Within a few years, the accuracy of observations will be sufficient to decide between the two interpretations of GR.

I'm betting on the simpler interpretation.

References

Damour, T. and Taylor, J.H. (1992), "Strong-field tests of relativistic gravity and binary pulsars", Phys.Rev.D 45:1840-1868. (See p. 1841.)

Danby, J.M.A. (1988), Fundamentals of Celestial Mechanics, 2nd edition, Willmann-Bell, Richmond.

Eddington, A.E. (1920), Space, Time and Gravitation, reprinted 1987 by Cambridge Univ. Press, Cambridge, 109.

Hatch, R.R. (1999), "Gravitation: Revising both Einstein and Newton", Galilean Electrodynamics 10#4:69-75.

Shapiro, I. et al. (1971), "Fourth test of general relativity: New radar results", Phys.Rev.Lett. 26:1132-1135.

Tom Van Flandern

Meta Research / Washington, DC

Our 1999 March 15 issue contained an article showing how general relativistic effects arise in flat-space-time theories. Regarding the classical tests of general relativity as it affects electromagnetic phenomena, we wish to cite the work of Fernando de Felice, “On the gravitational field acting as an optical medium”, Gen.Rel.&Grav. 2 #4, 347-357 (1971). The author notes that Einstein himself first suggested the idea that gravitation is equivalent to an optical medium. From the abstract, “… Maxwell’s equations may be written as if they were valid in a flat space-time in which there is an optical medium … this medium turns out to be equivalent to the gravitational field. … we find that the language of classical optics for the ‘equivalent medium’ is as suitable as that of Riemannian geometry.” Nine earlier authors who have worked on this problem are cited in the text.

In our MRB article, we placed special emphasis on the rotation of elliptical orbits (“perihelion motion”) because that particular effect had been much neglected in the prior literature dealing with flat-space-time treatments of this subject. We noted how Einstein’s own approach to getting the correct perihelion motion involved the combination of three effects, one of which cancels part of the contribution from the other two; and that it probably involved a trial-and-error approach to get the theory to correctly produce the known perihelion motion rate for Mercury. Certainly, Einstein’s choice is not unique.

By contrast, we argued that the simple, flat-space-time picture used by the Meta Model cosmology and inherent in LeSage-type (“pushing-particle”) models of gravitation implies a perihelion motion formula that comes out correctly from a single contribution – the velocity-slowing effect on masses that must be produced by any underlying light-carrying medium (LCM). In response to that article, we received reader feedback from two of you. [For this follow-up note, we will denote velocity by 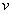rather than 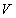. In the earlier article, was orbital true anomaly.]

Esko Lyytinen This email address is being protected from spambots. You need JavaScript enabled to view it. wrote:

“This brings up a point that sometimes has been on my mind while reading about models using a refracting medium. The main point is that, if the change of the density of the medium must be ‘tuned’ by the bending of light, then this is a small negative point for the theory. I am no proponent of GR (and am far from expert on it), especially as applied to the ‘inside’ of black holes. However, to be fair to GR, there the space-time curvature is considered to explain both light and what you call ‘ballistic motion’. For a refracting medium, it is intuitive to think about the density of the LCM changing with gravitational potential; but by how much exactly? If this is determined by observations of how light seems to behave, then there actually is another observable parameter in the theory. In the MRB article, on page 12, the light behavior is modeled using a potential-dependent factor 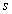, while the ballistic case uses the velocity dependent relativistic factor 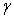. Can these be linked or derived from the same principle? (They are both somehow related to the density changes of the LCM.)”

and Victor Slabinski This email address is being protected from spambots. You need JavaScript enabled to view it. wrote:

“The recent paper ‘The Perihelion Advance Formula’ (MRB for March 15, 1999) starts off with a review of the LCM and how it can explain three different tests of GR (General Relativity). Then near the bottom of page 11, de Broglie matter waves are mentioned, in order to suggest that at least for electrons, the LCM index of refraction will affect their motion. [That notion suggests that LCM effects depend on the test-body composition; electrons constitute a larger fraction of the mass of hydrogen (one electron for each proton) than for helium (one electron for each proton and neutron).] But no further use is made of de Broglie waves; that paragraph could be omitted without affecting the argument or the readability.

“Near the top of page 12, the author notes that ‘the velocity of anything propagating through a medium is proportional to the square root of the medium density.’ So what? No further use is made of this fact. Next the LCM index of refraction is discussed. But in the middle of paragraph 3, out of nowhere, we have the statement “The relativistic clock-slowing ... is 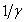...”. What does this have to do with the LCM? Nothing. The author himself says at the end of the paragraph ‘... and assume that 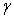is independent of the density of the LCM.’ So why is LCM discussed as part of perihelion advance?

“Finally on page 12, paragraph 4, the author assumes that 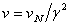. The whole derivation is really based on this formula. This is a velocity-dependence that has nothing to do with gravitational potential. On what ‘classical, flat-space-time principles’ [claim made inside front cover] is this formula based?”

My thanks to both readers for flagging these problems, which all stem from a single cause – a missing step in the logical development of ideas in my article. In the middle of the third paragraph on p. 12, we find these sentences: “But for the predominately ballistic motion of a planet or other body, the effect of the LCM is to slightly slow the ballistic velocity that the orbiting body would otherwise have because of its wave properties. The relativistic clock-slowing, meter-stick-contraction factor is 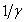, where 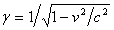, , and is the ballistic velocity of a body. Analogous to wave velocities being slowed by the factor 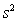, ballistic velocities are slowed by the factor 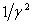” After the first and third sentences in this excerpt, one might well ask “why?” And in the answer to that lie the answers to all the other questions raised by these two readers.

In the early 19th century, it was widely realized that various transparent media influenced the speed of propagation of light. If it were not so, prisms and lenses would not function as they do. The optical theory of refraction depended for its successes on the speed of propagation of light being changed by optical media such as glass or water. When such speed measurements became possible, they confirmed this prediction of the theory.

How does this influence on the speed of light take place? At one extreme, the optical medium might temporarily become the light-carrying medium while light is in transit through it. In that case, the speed of light in a vacuum,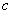 , would be reduced to the speed of light in the optical medium, . Also, the speed of any motion of the optical medium,http://www.metaresearch.org/cosmology2/gravity/PAFfolder/PerihelionAdvanceFormula-combined_files/image082.gif , would then add to or subtract from the speed of light through the medium,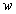 , to yield an observed speed of 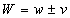relative to the non-moving laboratory. In other words, Galilean velocity addition rules would apply.

Alternatively, the LCM might be only somewhat affected, or entirely unaffected, by the motion of the matter which it permeates. We still assume (as observed) that a stationary optical medium slows the net light propagation speed from 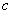to 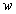, an effect classically referred to as “drag”. But when the medium is moving, the influence of the speed of the optical medium, 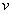, would be reduced by the influence factor 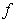, where 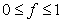, so that the measured speed of light relative to the laboratory would be 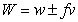. On principle alone, we might be inclined to guess that 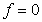in special relativity (SR), thereby assuring that the speed of light remains the same in all directions and independent of the speed of the optical medium. However, that is not in fact the prediction made by Einstein.

The correct formula for 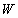was first predicted by Fresnel in 1817, and hence the phenomenon is known as “Fresnel drag”. It was confirmed experimentally using an interferometer by Fizeau in 1851. And the same formula was offered by Einstein for SR, derived from the Lorentz transformation for velocities. That correct formula is 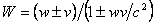. The upper sign applies when the optical medium and wave are moving in the same direction, and the lower sign when moving in opposite directions. For small values of 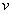, we see that 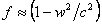, which is a small quantity (i.e., near zero) except for relatively dense optical media. This original prediction of Fresnel assumes an aether completely unaffected by the motion of the matter it permeates. In the sense that “space-time” is like an aether, Einstein’s prediction therefore has this same characteristic.

To apply this knowledge to the case at hand (LeSage-type models of gravity with a light-carrying medium), recall Feynman’s explanation of why light travels slower in a medium. A photon (whether particle or wave) always travels at speed 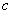, its vacuum speed, when it is propagating. But in an optical medium such as water or glass, the photon gets repeatedly absorbed and re-emitted by atoms encountered along its path. Each such event delays the photon’s forward progress because, while absorbed, the photon is moving at the atom’s mean speed 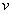instead of its own propagation speed 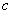. The accumulated effect of these absorption delays is what slows the net speed of the photon relative to the medium from 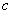down to 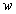. 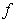then is the fraction of the time the wave spends absorbed by atoms instead of propagating. The mean delay between absorption and re-emission is typically a few nanoseconds. But since the speed of light is about a foot per nanosecond, photons in a medium can spend comparable time absorbed and carried along at speed 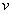as they spend propagating at speed . Still, during the very brief spurts between absorptions, light makes most of its progress because it travels so fast.

The “drag” effect is on the wave propagation speed, not on the underlying aether. In effect, whenever the wave is propagating, it’s speed is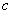 in a vacuum or 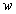in a stationary optical medium, where . (We assume that the wave makes no progress while it is absorbed by an atom when the medium is stationary.) But if the optical medium moves with speed , then the wave moves forward also at speed during the moments while it is absorbed by an atom. So the net speed is somewhat larger than when the medium moves in the same direction as the wave. Moreover, 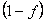is the fraction of the time the wave spends propagating, and is naturally inversely proportional to medium density when density is large because absorptions are then more frequent. Its proportionality to 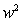therefore implies that wave speed should vary inversely with the square root of medium density, as has long been known empirically. It further implies that, for sparse media, 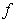would be directly proportional to medium density, which shows why the empirical rule breaks down for sparse media.

(Strictly, the net speed of the wave when not absorbed cannot always be simply c, as Feynman assumed. "Instantaneous" absorptions and discontinuities in speed are not very plausible, but are simply expressions of our ignorance of the details of the propagation and absorption processes. But gradual slowing of photons as they enter the strong electrostatic field of an atom would make more sense, especially in the LCM model. Whatever the details of the speed of propagation while a photon is between absorptions, the relation 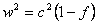is the one that must hold for consistency with the model being developed: However, no other use is made of the propagation speed 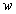while non-absorbed, so this detail is unimportant to the overall development.)

Now that we have refreshed on the concept of Fresnel drag, we are in a position to understand my allusions to the wave nature of matter. Focus on a single atom of matter. It is composed of a matter part moving ballistically (the protons and neutrons), and a wave part propagating through the LCM (the electrons). If initially the atom has no net speed 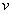relative to the LCM, then the electrons simply propagate back and forth with respect to the atomic nucleus at a wave propagation speed that is determined by the density of the LCM.

We have already seen (in the previous article) how that propagation speed changes if gravitational potential changes: The LCM gets denser near matter because of gravitational compression of the LCM. Equipotential surfaces become equi-density surfaces in the LCM. We can neglect an arbitrary additive constant for both potential at infinity and for LCM density at infinity. Only changes in potential or density can alter propagation speed and bend or delay the path of a propagating wave. So we have no need to “calibrate” this derivation using the Einstein light-bending effect.

Now imagine what would happen to the nucleus of an atom if its electrons stopped propagating and remained fixed in the aether. The atom would be forced to stop its motion and remain there also because of the strong electrostatic force between the electrons and the nucleus. For this reason, if forward electron propagation is slowed, the forward ballistic motion of the nucleus is slowed by a like amount. This, then, is the required linkage between the ballistic motion of matter and propagating wave motion through the aether. Note that this electrostatic interaction is entirely governed by charge, and is therefore independent of the masses of the particles involved.

But why do electrons slow their propagation speeds through the aether whenever the matter containing them moves? If the atom has a net speed 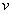relative to the LCM, it encounters more LCM per unit time than if it were stationary. It is just as if the LCM were denser. If the wave propagation speed is 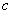and the matter speed is 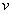, the increased density encountered per unit time is proportional to 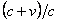. This effect is first-order in 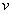, making it a much more significant effect than the aether density changes due to gravitational potential, which depend on .

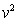Specifically, electrons are sometimes propagating in the same direction as the ballistic motion of the nucleus, in which case they encounter more LCM per unit time; and sometimes propagating in the opposite direction from the nucleus, in which case they encounter less LCM per unit time. The more LCM encountered, the greater its effective density, and the slower the electron propagates. And conversely. But the electron influences the nucleus because of the electrostatic force binding the two. So when something changes the speed of the propagating electron, the ballistic speed of the nucleus changes too.

It remains to comment on why the slowed propagation speed is proportional to 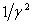. To answer fully requires a re-derivation of the Lorentz transformations for the LCM. Here, I will simply remark on the essence of that derivation. If light propagates at speed 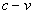relative to a source moving at speed 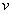over some fixed distance, and then travels the reverse path over the same distance at speed 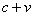relative to the same source, we can easily calculate the total distance traveled and the total elapsed time. From there, total distance divided by total time gives average speed, which is 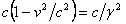. This is in fact how Einstein explained Fresnel drag. Physics might have taken a quite different course if Einstein had not then been set on eliminating the need for an aether.

In summary, electrons in matter propagate through the LCM at speed 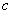determined by the local mean density of the LCM. The forward speed of the matter creates an effective increase in the density of the LCM by the factor 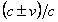, where the sign determines the direction of the matter with respect to the direction of electron propagation. This increased effective density slows the average propagation speed of the electrons by the factor 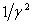. And the slowed electrons exert electrostatic force on the atoms to slow their forward ballistic speed by a like amount.

After reading this draft, Victor Slabinski posed the following specific questions, which I include here as part of the summary:

Q1) The light-carrying medium (LCM) has a density that depends on the gravitational potential. Please give the mathematical relation for this density.

A1) Wave velocity 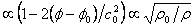. Here, 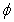is the potential and 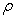the density of the medium at the wave location; and 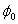is the potential, 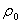the density, and 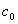the wave speed of the medium at the reference location, typically at infinity.

Q2) The speed of "matter waves" depends on the LCM density. Please give that relation.

A2) See above. In the notation of the original article, wave speed 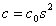, where 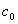is the speed of the wave at the reference location (e.g., infinity), and .

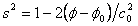Q3) Electrons in the atoms act as matter waves, so when the atom moves through the LCM, the matter wave speed of the electrons changes for “forward” and “backward” motion. Please give specific formulas for that.

A3) In the forward direction, speed is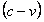 . In the backward direction, speed is 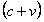. Average net speed is .

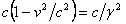Q4) This change in matter wave speed exerts a force on the atom; the resulting acceleration causes the perihelion advance. Please show how that force is produced and give a formula for it. (By Newton's laws, you need a force to produce a velocity change.)

A4) If electrons are slowed, the electrostatic force of the electrons has the same kind of effect on the nucleus of their atom as a change in the velocity of the Sun in its orbit around the galaxy would have on its own planets. In both cases, the latter are forced to follow the velocity changes in the former. In the case of atoms, this electrostatic force is entirely determined by charge, and is therefore independent of the masses of the particles involved.

Q – Analogy: I have a spaceship in elliptic orbit with a lot of interior marbles traveling fore and aft. The marble speed in the forward direction is less than the marble speed when they travel backwards. The speed difference depends on the spaceship orbital speed. Will the motion of the marbles produce a perihelion advance?

A – Analogy: Let's work on this analogy so that it fits the application. First, to eliminate any mass dependence, let the ship carry a positive charge, and the marbles a negative charge equal in the aggregate to the ship's positive charge. (We'd also better put the marbles outside the ship and give them plenty of angular momentum so they don't just stick to the hull.) Then anything affecting just the ship or just the marbles will end up affecting both because of the electrostatic force between them. Now, if something slows the marbles more at perihelion than at aphelion, yes, that would advance the perihelion of the spaceship’s solar orbit.

Sometimes, a lot of physics can be hidden behind a seemingly innocent statement such as the one I quoted at the start of this note. But I hope the preceding provides the needed justification for the unintended “leap of logic” in that one step of our March 15 article.