Does space curve?

[Excerpt from T. Van Flandern (2002), "Does gravity have inertia?", Meta Research Bulletin 11, 49-53.]

Some relativists may argue that “space-time” is not simply space plus time, but a higher-level concept that includes the notion of “time”, so the physical principles do not apply. However, the physical principles arise from logic alone and should be immutable, in contrast to the laws of physics, which can change as knowledge improves [[i]]. Moreover, “space-time” is a mathematical concept, which amounts to a fancy way of referring to proper time in relativity (the time kept by perfect clocks), and does not involve any curvature of space. To show this, consider the following mathematical and physical arguments.

Let dT be a coordinate time interval (an idealized time in some specific reference frame) for a moving body, and let (dX, dY, dZ) be the change in the body’s space coordinates during that time interval. Next, let ds be a path length in “space-time” for the body during the same interval; and let c be the speed of light. Then the standard relation between space, time, and “space-time” (with no gravity acting) is:

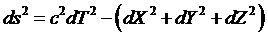
Multiplying the coordinate time interval by the speed of light has turned time into a length-like coordinate (meaning a time interval measured in meters, not to be confused with a "space-like interval" as used in GR). This change of units allows the time interval to be combined with the coordinates for the three spatial dimensions. However, the presence of a minus sign makes the combination un-length-like; i.e., not the equivalent of space plus time treated as comparable length-like coordinates. So to see the physical meaning of the space-time parameter s, first note that the parentheses enclose the square of the distance traveled by the body. But distance is just velocity v times the time interval dT: 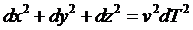. So our first equation above becomes:.

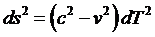Moreover, if the body travels through a gravitational field having potential f (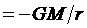; note the minus sign, following the astronomical convention wherein potentials are negative) at a distance r from a source mass M, then s is a “curved” space-time path length along a geodesic path (a free-fall path through a gravitational field), and our preceding formula generalizes to what is called the “Schwarzschild metric”:

In this form, we can see the space-time interval ds as a purely time-like interval dt that was merely made to look length-like through multiplying it by c. This is what we mean by saying that curved space-time does not involve a curvature of space. The only effects in the relation between coordinate time and “space-time” are the clock-slowing effects of velocity and gravitational potential.

Because this point is of some importance, we will illustrate it physically as well. Consider the geodesic (orbital) path of the Earth with respect to the Sun in Figure 1. If we choose any two points along that path (call them A and B), note that a straight line between A and B (as could be represented by a taut rope) is a shorter path through space than the geodesic path. Precisely the same remarks would be true if the Earth were replaced by a photon whose path is bent with respect to space as it passes the Sun – a taut rope takes a shorter path through space than the photon does. The extra bending is most easily explained as a refraction effect in the space-time or light-carrying medium [[ii],[iii]]. This again illustrates that “curved space-time” geodesic paths do not involve any curvature of space.

The contrary viewpoint in many textbooks has been a source of confusion for physics students for the last generation. For an extreme expression of this contrary viewpoint in support of the geometric interpretation of GR, see opinions by Robert Wald [ [iv]]. Yet the fact that space does not curve just because "space-time" does would come as a surprise to many students of the history of relativity, who tend to think as Riemann did. However, even in Misner, Thorne & Wheeler's text that popularized the geometric interpretation of GR [[v]], we find the following caution: "But if there was one reason more than any other why [Riemann] failed to make the decisive connection between gravitation and curvature, it was this, that he thought of space and the curvature of space, not of spacetime and the curvature of spacetime."

This is an important concept. If the curved path of a body through space is not caused by a curvature of space, then space remains Euclidean (flat) and an external force is still required to produce and explain any deviation from straight line motion. Moreover, some explanation other than curved space is needed to understand the equivalence-principle-like property of gravity.

[i]? T. Van Flandern (2001), “Physics has its principles”, in Gravitation, Electromagnetism and Cosmology, K. Rudnicki, ed., C. Roy Keys Inc., Montreal, 87-101; also (2000), MetaRes.Bull. 9: 1-9.

[ii] Sir A. Eddington (1920), Space, Time and Gravitation, Cambridge Univ. Press (reprinted 1987), Cambridge, 109

[iii] T. Van Flandern (2002), “Gravity”, in Pushing Gravity: New Perspectives on Le Sage’s Theory of Gravitation, Apeiron, Montreal, 93-122.

[iv]R.M. Wald (1984), General Relativity, U. of Chicago Press, Chicago, 67.

[v] C.W. Misner, K.S. Thorne & J.A. Wheeler (1973), op.cit., 32-33.